8.2. Уравнение газового состояния
8.16. В цилиндр длиной l = 1,6 м, заполненный воздухом при нормальном атмосферном давлении p0, начали медленно вдвигать поршень площадью S = 200 см2. Определить силу F, которая будет действовать на поршень, если его остановить на расстоянии l1 = 10 см от дна цилиндра.
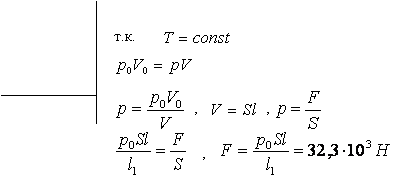 Дано: Решение:
Дано: Решение:
l = 1,6 м
p0
S = 0,02 см2
l1 = 0,1 м
F – ?
Ответ: 32,3×103 H
8.17. Колба вместимостью V = 300 см2, закрытая пробкой с краном, содержит разреженный воздух. Для измерения давления в колбе горлышко колбы погрузили в воду на незначительную глубину и открыли кран, в результате чего в колбу вошла вода массой т = 292 г. Определить первоначальное давление p в колбе, если атмосферное давление p0 = 100 кПа.
 Дано: Решение:
Дано: Решение:
V = 300 см2
т = 0,292 кг
p0 = 105 Па
p – ?
Ответ: 2,67×103 Па
8.18. В U-образный манометр налита ртуть. Открытое колено манометра соединено с окружающим пространством при нормальном атмосферном давлении p0, и ртуть в открытом колене стоит выше, чем в закрытом, на ∆h = 10 см. При этом свободная от ртути часть трубки закрытого колена имеет длину l = 20 см. Когда открытое колено присоединили к баллону с воздухом, разность уровней ртути увеличилась и достигла значения ∆h1 = 26 см. Найти давление p воздуха в баллоне.
 Дано: Решение:
Дано: Решение:
∆h = 0,1 см
p0
l = 0,2 м
∆h1 = 0,26 м
p – ?
Ответ: 47,2×103 Па
8.19. Манометр в виде стеклянной U-образной трубки с внутренним диаметром d = 5 мм (см.рис. ниже, а) наполнен ртутью так, что оставшийся в закрытом колене трубки воздух занимает при нормальном атмосферном давлении объем V1 = 10 мм3. При этом разность уровней ∆h ртути в обоих коленах трубки равна 10 см. При соединении открытого конца трубки с большим сосудом (см. рис.ниже, б) разность ∆h2 уровней ртути уменьшилась до 1 см. Определить давление p в сосуде.
 Дано: Решение:
Дано: Решение:
d = 0,005 м
V1 = 10-9 мм3
∆h = 0,1 м
∆h2 = 0,01 м
p – ?
Ответ: 2,3×103 Па
8.20. В баллоне содержится газ при температуре t1 = 100 °С. До какой температуры t2 нужно нагреть газ, чтобы его давление увеличилось в два раза?
 Дано: Решение:
Дано: Решение:
t1 = 100 °С
t2 – ?
Ответ: 2000 С