3.36. В центре скамьи Жуковского стоит человек и держит в руках стержень длиной l = 2,4 м и массой т = 8 кг, расположенный вертикально по оси вращения скамейки. Скамья с человеком вращается с частотой п1 = 1с-1. С какой частотой п2 будет вращаться платформа, если человек перейдет в ее центр? Суммарный момент инерции J человека искамьи равен 6 кг×м2 .
 Дано: Решение:
Дано: Решение:
l = 2,4 м
т = 8 кг
п1 = 1с-1
J = 6 кг∙м2
п2 - ?
Ответ: 0,61 с-1
3.37. Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья неподвижна, колесо вращается с частотой n = 10 с-1. Радиус R колеса равен 20 см. его масса m = 3 кг. Определить частоту вращения п1 скамьи, если человек повернет стержень на угол 180°? Суммарный момент инерции J человека и скамьи равен 6 кг×м2. Массу колеса можно считать равномерно распределенной по ободу.
Дано: Решение:
 n = 10 с-1
n = 10 с-1
R = 20 см
m = 3 кг
φ = 180°
J = 6 кг×м2
n2 - ?
Ответ: 0,4 с-1
3.4. Работа и энергия
3.38. Шарик массой т = 100 г, привязанный к концу нити длиной l1 = 1 м, вращается, опираясь на горизонтальную плоскость, с частотой п1 = 1 с-1. Нить укорачивается и шарик приближается к оси вращения до расстояния l2 = 0,5 м. С какой частотой п2 будет при этом вращаться шарик? Какую работу А совершит внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.
Дано: Решение:
 т = 100 г
т = 100 г
l1 = 1 м
l2 = 0,5 м
п1 = 1 с-1
l2 = 0,5 м
п2 - ?
А -?
Ответ: 5,92 Дж ; 4 с-1
3.39. Маховик вращается по закону, выражаемому уравнением j = A+Bt+Ct2, где А = 2 рад, В = 32 рад/с, С = –4
рад/с2. Найти среднюю мощность ![]() , развиваемую силами, действующими
на маховик при его вращении, до остановки, если его момент инерции J= 100 кг×м2.
, развиваемую силами, действующими
на маховик при его вращении, до остановки, если его момент инерции J= 100 кг×м2.
 Дано: Решение:
Дано: Решение:
j = A+Bt+Ct2
А = 2 рад
В = 32 рад/с
С = –4 рад/с2
J= 100 кг×м2
![]() - ?
- ?
Ответ: 3200 Вт ; -800 Вт/с
3.40. Маховик вращается по закону, выражаемому уравнением j = А + Bt + Ct2, где А = 2 рад, В = 16 рад/с, С = –2 рад/с2. Момент инерции J маховика равен 50 кг×м2. Найти законы, по которым меняются вращающий момент М и мощность N. Чему равна мощность в момент времени t = 3 с?
Дано: Решение:
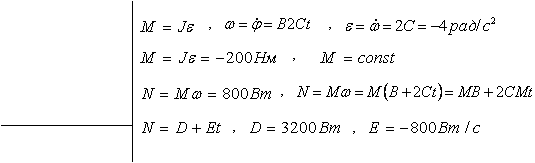 j = А + Bt + Ct2
j = А + Bt + Ct2
А = 2 рад
В = 16 рад/с
С = –2 рад/с2
J = 50 кг×м2
t = 3 с
М - ?
N - ?
Ответ: 3200 Вт ; -800 Вт/с