3.26. Два тела массами m1 = 0,25 кг и m2 = 0,15 кг связаны тонкой нитью, переброшенной через блок (см. рис. ниже). Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой т1 С каким ускорением а движутся тела и каковы силы T1 и T2 натяжения нити по обе стороны от блока? Коэффициент трения f тела о поверхность стола равен 0,2. Масса m блока равна 0,1 кг и ее можно считать равномерно распределенной по ободу. Массой нити и трением в подшипниках оси блока пренебречь.
 Дано: Решение:
Дано: Решение:
m1 = 0,25 кг
m2 = 0,15 кг
f = 0,2
m = 0,1 кг
а – ?
T1 – ?
T2 – ?
Ответ: 1,97 м/с2
3.27. Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m1 = 0,3 кг и m2 = 0,5 кг. Определить силы натяжения T1 и T2 шнура по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.
 Дано: Решение:
Дано: Решение:
m = 0,2 кг
m1 = 0,3 кг
m2 = 0,5 кг
T1 – ?
T2 – ?
Ответ: T1 = 3,53 Н ; T2 = 3,92 Н
3.28. Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид j = А + Bt2 + Ct3, где В = 4 рад/с2, С = –1 рад/с3. Найти закон изменения момента сил, действующих на шар. Определить момент сил М в момент времени t = 2 с.
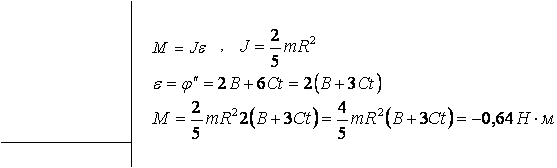 Дано: Решение:
Дано: Решение:
m = 10 кг
R = 0,2 м
j = А + Bt2 + Ct3
В = 4 рад/с2
С = –1 рад/с3
t = 2 с
М – ?
Ответ: - 0,64 Н×м
3.3. Закон сохранения момента импульса
3.29. Однородный тонкий стержень массой m1 = 0,2 кг и длиной l = 1 м может свободно вращаться вокруг горизонтальной оси z, проходящей через точку О (см.рис.ниже). В точку А на стержне попадает пластилиновый шарик, летящий горизонтально (перпендикулярно оси z) со скоростью v = 10 м/с и прилипает к стержню. Масса m2 шарика равна 10 г. Определить угловую скорость w стержня и линейную скорость и нижнего конца стержня в начальный момент времени. Вычисления выполнить для следующих значений расстояния между точками А и О: 1) l/2; 2) l/3; 3) l/4.
 Дано: Решение:
Дано: Решение:
m1 = 0,2 кг
l = 1 м
v = 10 м/с
m2 = 0,01 кг
1) l/2
2) l/3
3) l/4
w – ?
и – ?
|
Ответ: 1) 0,839 рад/с ; 0,629 м/с ; 2) 1,43 м/с; 0,952 м/с ; 3) 0,833 рад/с ; 0,625 м/с
3.30. Однородный диск массой m1 = 0,2 кг и радиусом R = 20 см может свободно вращаться вокруг горизонтальной оси z, перпендикулярной плоскости диска и проходящей через точку О (см. рис. ниже). В точку А на образующей диска попадает пластилиновый шарик, летящий горизонтально (перпендикулярно оси z) со скоростью v = 10 м/с, и прилипает к его поверхности. Масса m2 шарика равна 10 г. Определить угловую скорость w диска и линейную скорость и точки В на диске в начальный момент времени. Вычисления выполнить для следующих значений а и b: 1) а = b = R; 2) а = R/2, b = R; 3) a = 2R/3, b = R/2; 4) а = R/3, b = 2R/3.
 Дано: Решение:
Дано: Решение:
m1 = 0,2 кг
R = 20 см
v = 10 м/с
m2 = 10 г
1) а = b = R
2) а = R/2
b = R
3) a = 2R/3
b = R/2
4) а = R/3
b = 2R/3
w - ?
и - ?
Ответ: 4,55 рад/с ; 0,909 м/с ; 2) 2,27 рад/с ; 0,454 м/с ;3) 1,52 рад/с ; 0,202 м/с