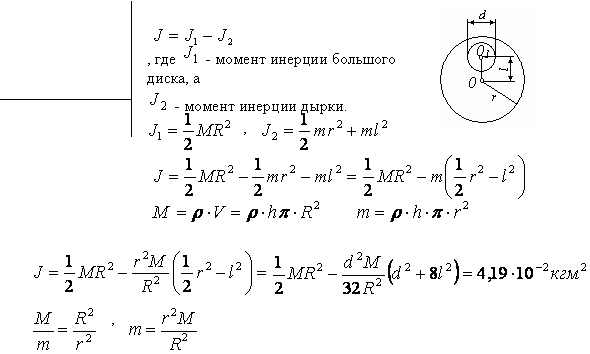
3.16. В однородном диске массой т = 1 кг и радиусом r = 30 см вырезано круглое отверстие диаметром d = 20 см, центр которого находится на расстоянии l = 15 см от оси диска (см. рис. ниже). Найти момент инерции J полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.
 Дано: Решение:
Дано: Решение:
т = 1 кг
r = 0,3 м
d = 0,2 м
l = 0,15 м
,
J – ?
Ответ: 4,19-2 кг×м2
3.17. Найти момент инерции J плоской однородной прямоугольной пластины массой т = 800 г относительно оси, совпадающей с одной из ее сторон, если длина а другой стороны равна 40 см.
 Дано: Решение:
Дано: Решение:
т = 0,8 кг
а = 0,4 м
J – ?
Ответ: 4,27-2 кг×м2
3.18. Определить момент инерции J тонкой плоской пластины со сторонами а = 10 см и b = 20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью s = 1,2 кг/м2.
 Дано: Решение:
Дано: Решение:
а = 0,1 м
b = 0,2 м
s = 1,2 кг/м2
J – ?
Ответ: 2×10-5 кг×м2
3.2. Основное уравнение динамики вращательного движения
3.19. Тонкий однородный стержень длиной l = 1 может свободно вращаться вокруг горизонтальной оси, проходящей через точку О на стержне (см. рис. ниже). Стержень отклонили от вертикали на угол a и отпустили. Определить для начального момента времени угловое e и тангенциальное аt ускорения точки В на стержне. Вычисления произвести для следующих случаев: 1) а = 0, b = 2/3l, a = p/2; 2) а = l/3, b = l, a = p/3; 3) а = l/4, b = l/2, a = 2/Зp.
 Дано: Решение:
Дано: Решение:
l = 1
1) а = 0
b = 2/3l
a = p/2
2) а = l/3
b = l
a = p/3
3) а = l/4
b = l/2
a = 2/Зp
аt – ?
e – ?
Ответ: 1) 14,7 рад/с2; 9,8 м/с2 2) 12,7 рад/с2; 8,49 м/с2 3) 14,6 рад/с2 ; 3,64 м/с2
3.20. Однородный диск радиусом R = 10 см может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем (см.рис.ниже). Диск отклонили на угол a и отпустили. Определить для начального момента времени угловое e и тангенциальное аt ускорения точки В, находящейся на диске. Вычисления выполнить для следующих случаев: 1) а = R, b = R/2, a = p/2; 2) а = R/2, b= R, a = p/6, 3) а = 2/ЗR, b = 2/ЗR, a = 2/Зp.
 Дано: Решение:
Дано: Решение:
R = 0,1 м
1) а = R
b = R/2
a = p/2
2) а = R/2
b= R
a = p/6
3) а = 2/ЗR
b = 2/ЗR
a = 2/Зp
e – ?
аt – ?
|
Ответ: 1) 65,3 рад/с2 ; 9,8 м/с2 2) 32,7 рад/с2 ; 4.9 м/с2 3) 7,99 рад/с2 ; 59,9 м/с2