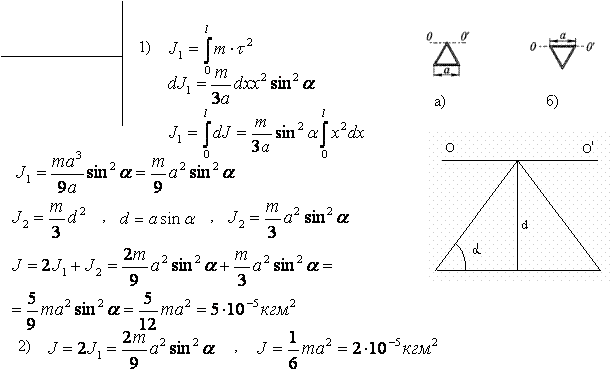
3.11. Определить момент инерции J проволочного равностороннего треугольника со стороной а = 10 см относительно: 1) оси, лежащей в плоскости треугольника и проходящей через его вершину параллельно стороне, противоположной этой вершине (см. рис. ниже, а); 2) оси, совпадающей с одной из сторон треугольника (см. рис. ниже, б). Масса т треугольника равна 12 г и равномерно распределена по длине проволоки.
Дано: Решение:
а = 0,1 м
т = 0,012 кг
J – ?
Ответ: 5×10-5 кг×м2 ; 2×10-5 кг×м2
3.12. На концах тонкого однородного стержня длиной l и массой 3m прикреплены маленькие шарики массами m и 2m. Определить момент инерции J такой системы относительно оси, перпендикулярной стержню и проходящей через точку О, лежащую на оси стержня. Вычисления выполнить для случаев а, б, в, г, д, изображенных на рис ниже. При расчетах принять l = 1 м, m = 0,1 кг. Шарики рассматривать как материальные точки.
Дано: Решение:
l = 3m
m
2m
l = 1 м
m = 0,1 кг
J – ?
|
г)д)
Ответ: 0,3 кг×м2 ;0,0833 кг×м2
3.13. Найти момент инерции J тонкого однородного кольца радиусом R = 20 см и массой m = 100 г относительно оси, лежащей в плоскости кольца и проходящей через его центр.
Дано: Решение:
R = 0,20 м
m = 0,1 кг
J – ?
Ответ: 0,002 кг×м2
3.14. Определить момент инерции J кольца массой т = 50 г и радиусом R= 10 см относительно оси, касательной к кольцу.
Дано: Решение:
т = 0,05 кг
R= 0,1 м
J – ?
Ответ:
3.15. Диаметр диска d = 20 см, масса т = 800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.
Дано: Решение:
d = 0,2 м
т = 0,8 кг
J – ?
Ответ: 6×10-3 кг/м2
