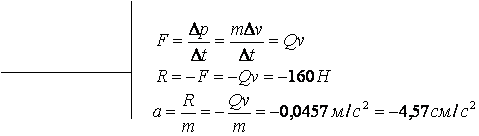
2.16. Космический корабль имеет массу m = 3,5 т. При маневрировании из его двигателей вырывается струя газов со скоростью v = 800 м/с; расход горючего Qm = 0,2 кг/с. Найти реактивную силу R двигателей и ускорение а, которое она сообщает кораблю.
Дано: Решение:
m = 3500 кг
v = 800 м/с
Qm = 0,2 кг/с
R – ?
а – ?
Ответ: -160 Н ; -4,57 см/с2
217. Вертолет массой m = 3,5 т с ротором, диаметр d которого 18 м, «висит» в воздухе. С какой скоростью v ротор отбрасывает вертикально вниз струю воздуха? Диаметр струи считать равным диаметру ротора.
Дано: Решение:
m = 3500 т
d = 18 м
dC = 18 м
v – ?
Ответ: 10,2 м/с .
2.18.Брусок массой m2 = 5 кг может свободно скользить по горизонтальной поверхности без трения. На нем находится другой брусок массой m1 = 1 кг. Коэффициент трения соприкасающихся поверхностей брусков f = 0,3. Определить максимальное значение силы .Fmax приложенной к нижнему бруску, при которой начнется соскальзывание верхнего бруска.
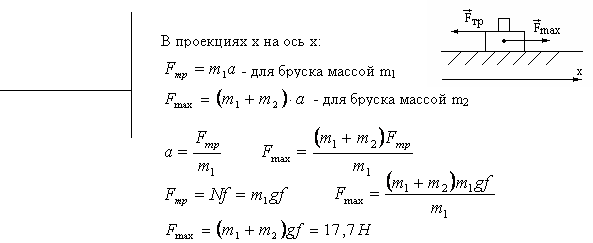Дано: Решение:
m2 = 5 кг
m1 = 1 кг
f = 0,3
Fmax – ?
Ответ: 17,7 Н .
2.19. На горизонтальной поверхности находится брусок массой m1= 2 кг. Коэффициент трения f1 бруска о поверхность равен 0,2. На бруске находится другой брусок массой т2= 8 кг. Коэффициент трения f2 верхнего бруска о нижний равен 0,3. К верхнему бруску приложена сила F. Определить: 1) значение силы F1 при котором начнется совместное скольжение брусков по поверхности; 2) значение силы F2, при котором верхний брусок начнет проскальзывать относительно нижнего.
Дано: Решение:
m1= 2 кг
f1 = 0,2
т2= 8 кг
f2 = 0,3
1) F1 – ?
2) F2 – ?
Ответ: 19,6 Н ; 39,2 Н .
2.20. Ракета, масса которой М = 6 т, поднимается вертикально вверх. Двигатель ракеты развивает силу тяги F = 500 кН. Определить ускорение а ракеты и силу Т натяжения троса, свободно свисающего с ракеты, на расстоянии, равном 1/4 его длины от точки прикрепления троса. Масса m троса равна 10 кг. Силой сопротивления воздуха пренебречь.
Дано: Решение:
М = 6000 кг
F = 500∙103 Н
r =1/4∙l
m = 10 кг
а – ?
Т – ?
Ответ:
