13.11. Расстояние l между свободными зарядами = 180 нКл и  = 720 нКл равно 60 см. Определить точку на прямой, проходящей через заряды, в которой нужно поместить третий заряд  так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда. Устойчивое или неустойчивое будет равновесие?

 

Дано:                                      Решение:

l=0,6 м

= Кл

= Кл

  

-?  х-?

 

 

 

 

                            Только

 

 

      

 

 

 

 

 

 

 

 

 

 

 

 

 

      

 

 

 

 

 

 

 

 

 

 

   

 

 

 

	То силы изменяться по

 

 

 

 

Ответ:  (м); = (Кл).

 

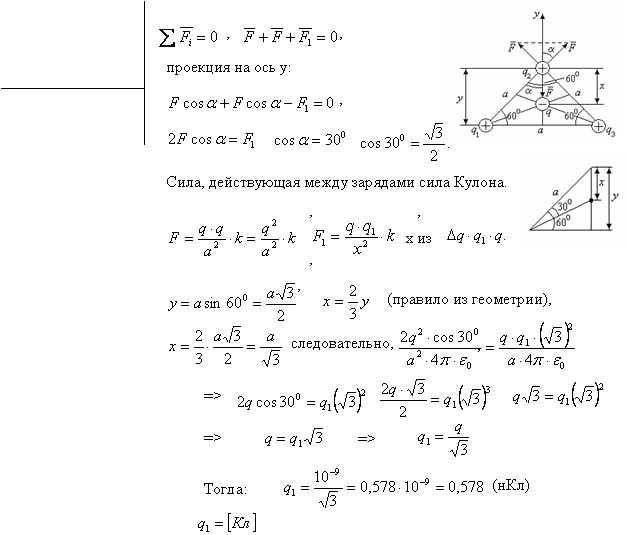
13.12. Три одинаковых заряда Q=1 нКл каждый расположены по вершинам  равностороннего треугольника. Какой отрицательный заряд  нужно поместить в центре треугольника, чтобы его притяжение уравновесило силы взаимного отталкивания зарядов? Будет ли это равновесие устойчивым?

 

Дано:                                      Решение:       

Q= Кл

а,

 

-?                                                                                                                                                                                    

                                                                                                                     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ:  (нКл), т.к. заряд поместили отрицательный, равновесие не устойчивое.

 

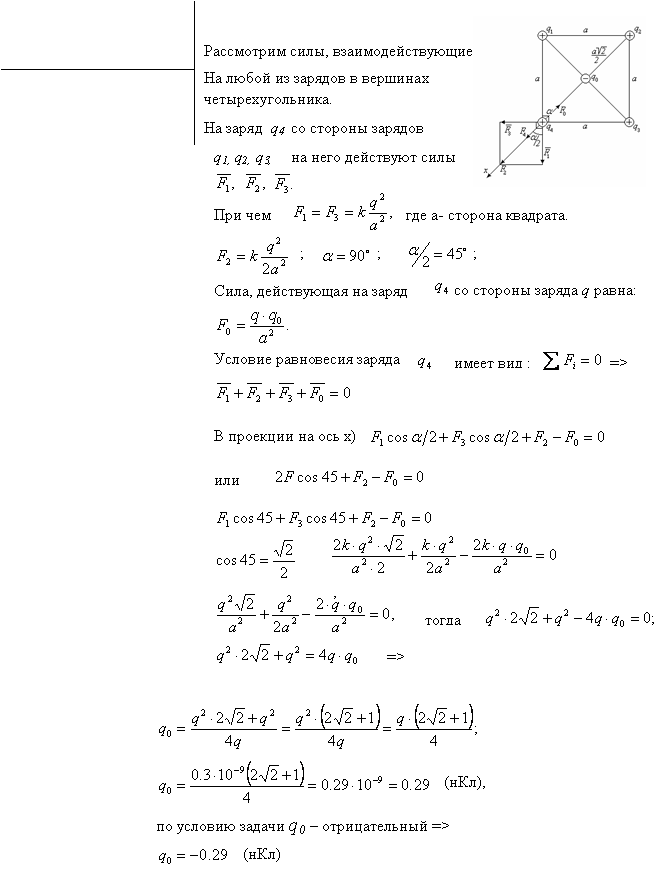
13.13. В вершинах квадрата находятся одинаковые заряды Q= 0,3 нКл каждый. Какой отрицательный заряд  нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

 

Дано:                                                 Решение:

Q=Q₁=Q₂=Q₃=Q₄=0.3нКл

а₁=а₂=а₂=а₃=а

                 

Q₀-?

 

 

 

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                  

 

 

 

                                  

 

 

                                  

 

 

 

                                  

 

 

 

  

 Ответ: (нКл)

 

Взаимодействие точечного заряда с зарядом, равномерно распределенным

 

13.14. Тонкий стержень длиной l=10 см равномерно заряжен. Линейная плотность  заряда равна 1мкКл/м. На продолжении оси стержня на расстоянии а=20 см от ближайшего его конца находится точечный заряд Q=100 нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.

 

Дано:                          Решение:

l=0,1 м                      

= Кл/м

а=0,2 м

Q= Кл

 

F-?

 

 

 

 

 

 

 

 

 

 

 

Ответ:    (мН)              

 

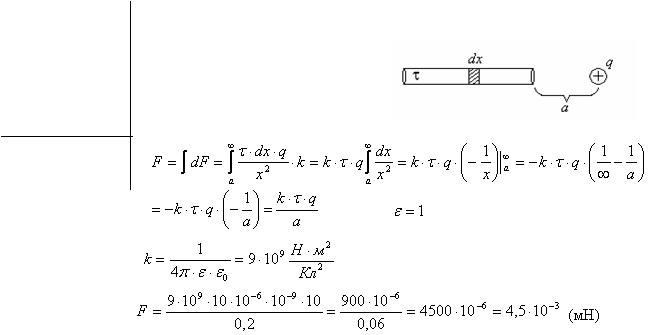
13.15. Тонкий длинный стержень равномерно заряжен с линейной плотностью  заряда, равной 10 мкКл/м. На продолжении оси стержня на расстоянии а=20 см от его конца находится точечный заряд Q=10 нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.

 

Дано:                          Решение:

= Кл/м        , т.е. , 

а=0,2 м                      , т.к.  , тогда 

Q= Кл            =>

  F-?                             

                                   

 

 

 

 

 

 

 

 

 

 

Ответ:  (мН)