1.2. Криволинейное движение
1.26. Материальная точка движется по плоскости согласно уравнению 
.
Написать зависимости: 1) v(t),
2) a(t).
Дано: Решение:
1) v(t) – ?
2) a(t) – ?
Ответ: V=3iAt2+2jBt , a=6iAt+2jB
1.27. Движение материальной точки задано уравнением
,где A=0,5
м, 
=
5 рад/с. Начертить траекторию точки. Определить модуль скорости 
и модуль нормального
ускорения 
.
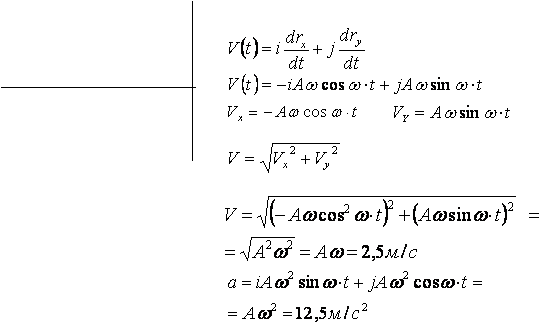Дано: Решение:
A=0,5 м
=
5 рад/с
– ?
– ?
Ответ: 2.5 м/с , 12,5 м/с.
1.28. Движение материальной точки задано уравнением 
, где А = 10 м, В = –5 м/с2, С = 10 м/с. Начертить траекторию точки. Найти выражения v(t) и a(t). Для момента времени t = 1
с вычислить: 1) модуль скорости ; 2)модуль ускорения 
; 3) модуль тангенциального
ускорения 
4)
модуль нормального ускорения .
Дано: Решение:
А = 10 м
В = –5 м/с2
С = 10 м/с
t = 1 с
v(t) – ?
a(t) – ?
1) – ?
2) – ?
3) – ?
4) – ?
Ответ:
1.29. Точка движется по кривой с постоянным тангенциальным
ускорением 
=
0,5 м/с2. Определить полное ускорение a
точки на участке кривой с радиусом кривизны R = 3 м, если точка движется на этом участке со скоростью v = 2 м/с.
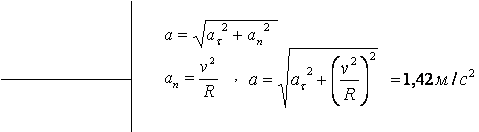Дано: Решение:
= 0,5
м/с2
R = 3 м
v = 2 м/с
a – ?
Ответ:1,42 м/с2
1.30. Точка движется по окружности радиусом R
= 4 м. Начальная скорость v0 точки
равна 3 м/с, тангенциальное ускорение 
= 1 м/с2. Для момента времени t = 2 с определить:1) длину пути s,
пройденного точкой; 2) модуль перемещения 
; 3) среднюю путевую скорость 
; 4) модуль вектора
средней скорости 
.
Дано: Решение:
R = 4 м
v0 = 3 м/с
= 1
м/с2
t = 2 с
1) s – ?
2) – ?
3) – ?
4) – ?
Ответ:
